I've been obsessed recently with the work of Nils Aall Barricelli who pioneered cellular automata 15 years before John Conway, artificial life 20 years before Christopher Langton and chaos theory 15 years before Benoit Mandelbrot. Barricelli called his creation "symbioorganisms", but it's interesting to try to demystify them without any analogies with living organisms.

The playing field is a finite, circular 1D space of discrete squares. Squares can be occupied by one of many different kinds of elements. Each kind of element has a propensity to move through the space with a constant step. To this space of elements striding around, Barricelli adds 3 rules. (Well, he experimented with many different tweaks in his papers, but this is one concrete, elegant formulation.)

• Destruction: When two objects collide, delete both. (This isn't quite what Barricelli says. But it suffices!)
• Creation: When an object A moves to where a second object B used to be, make a new copy of it, somewhere nearby that depends on B.
• Mutation: This rule is slightly more difficult to explain, and I found the rules plenty interesting without using it in this post. In brief, empty squares sometimes create new kinds of elements.

Just adding the first 2 rules gives rise to some very interesting behavior. Here's a pretty picture:

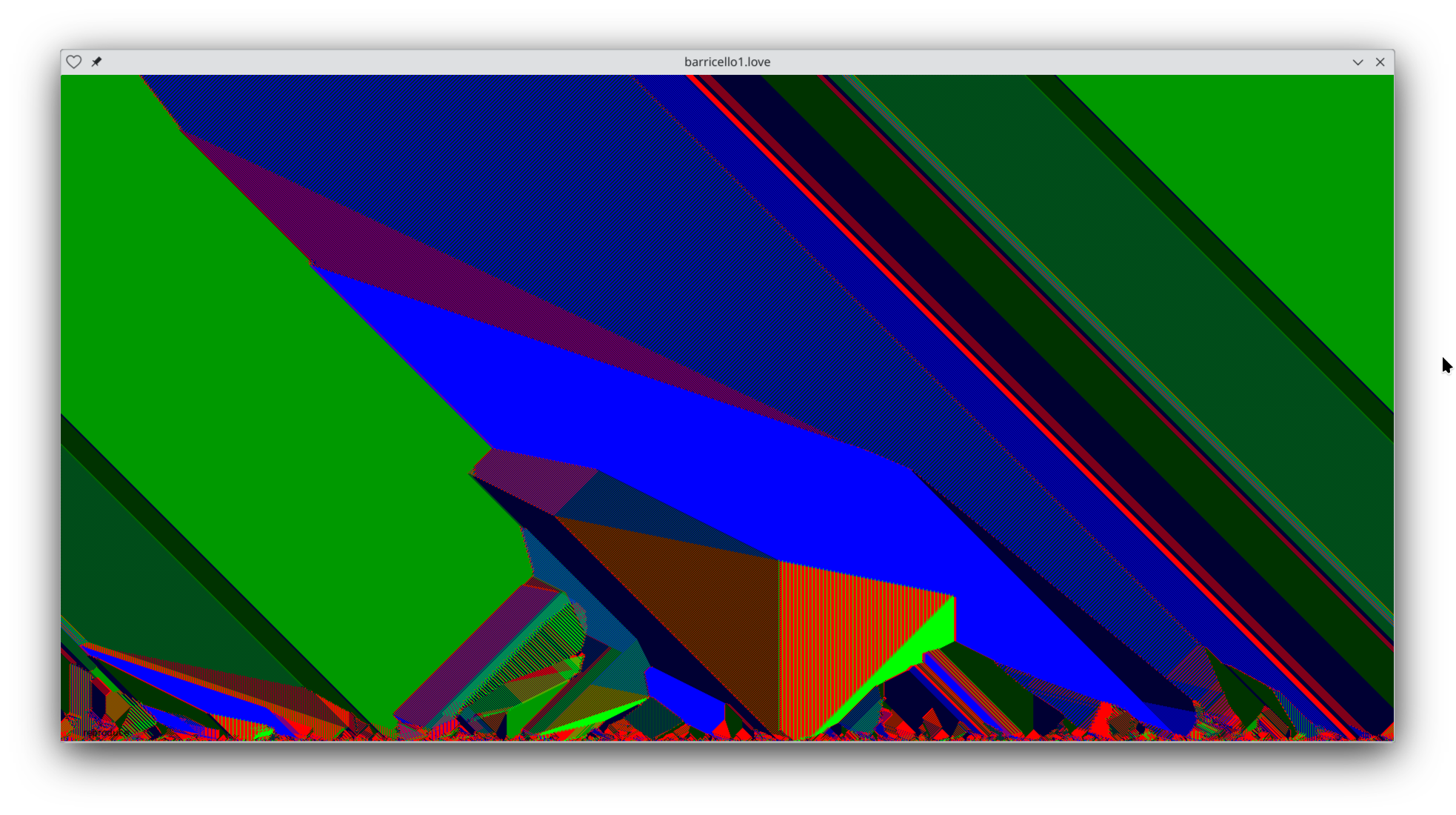
In this picture, each row of pixels represents the state of the space at one point in time. Time moves from the bottom of the picture to the top. The space is seeded randomly with a few different kinds of elements. Elements that stride rightward are colored shades of green. Elements that stride leftward are colored shades of blue. Red pixels are empty squares.

This picture shows that at the start we have a lot more differences in color, but in a few generations the "populations" (coherent bands of color) quickly become more stable.

Zooming in, we see that what looks like flat shades of color are really extremely regular patterns of the different kinds of elements. These are Barricelli's "symbioorganisms".

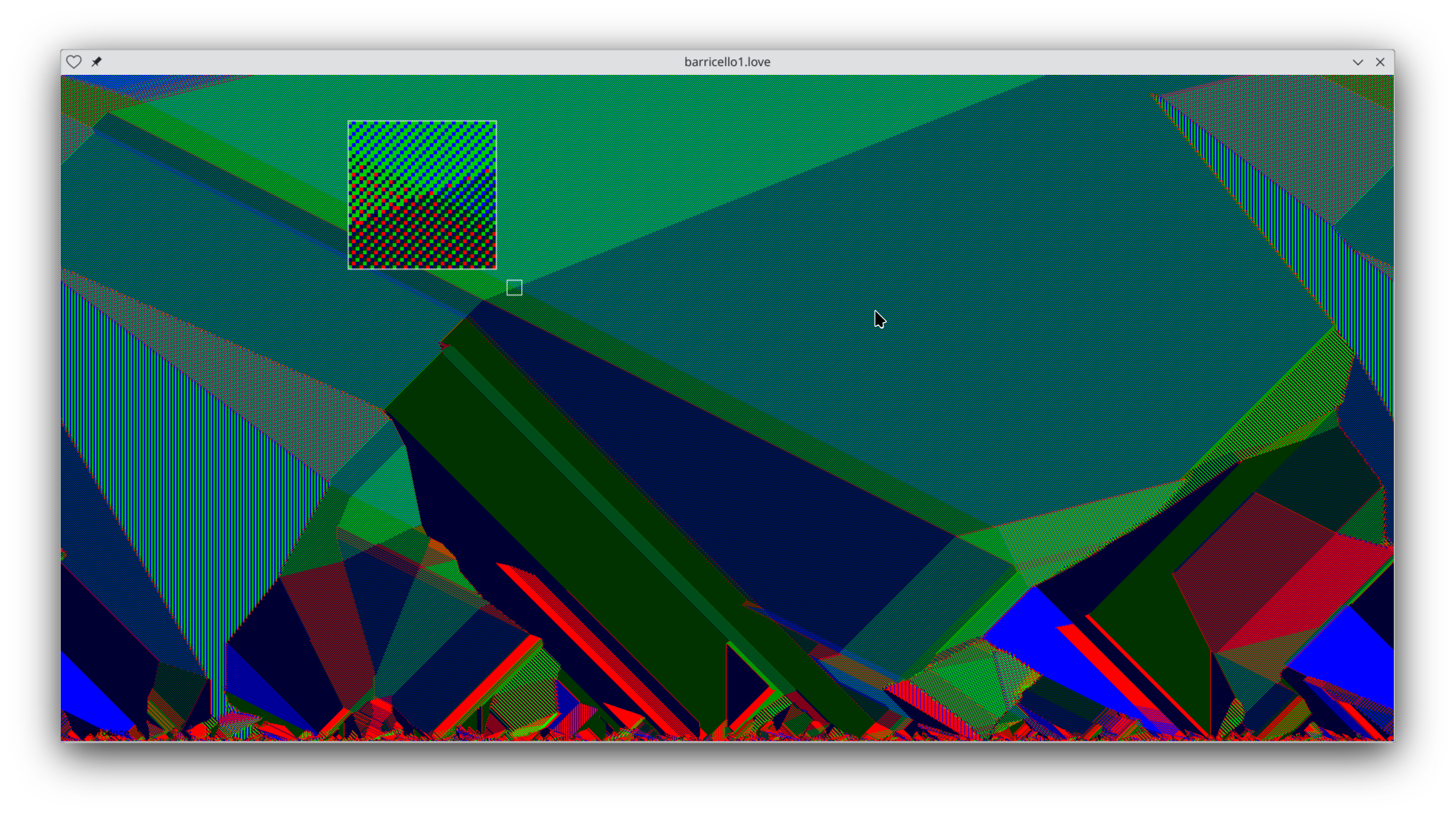
How could this be? The different colors of elements stride in different directions at different rates. How do stable patterns emerge? Here's one example that shows what's going on:

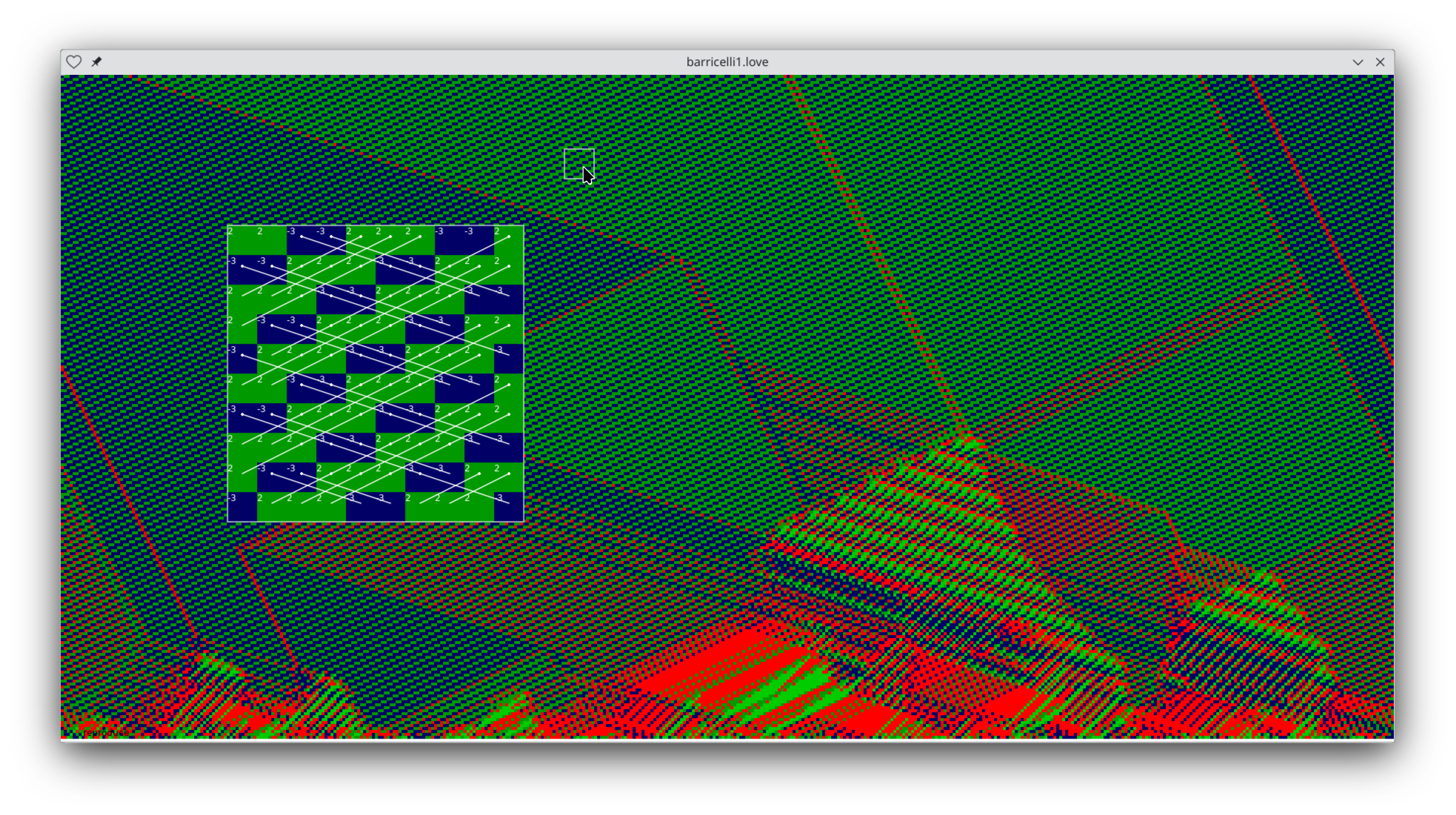
Here I've annotated the zoomed-in view with each element's stride, and lines showing each element's motion. The blues (B) move 3 squares left per time step, while the greens (G) move 2 steps right. However, a configuration of BBGGG is stable with just these rules. Each pair of blues "switches partners" with a different triple of greens going the other way. The effect is of a stable periodic pattern with a period of 5 squares.

I've tried many different random initial conditions, and such periodic patterns always occur. Barricelli calls this phenomenon "spontaneous generation", and it is remarkably robust. The BBGGG pattern above is nowhere near the only possible organism. Another simple one is BBBGG:

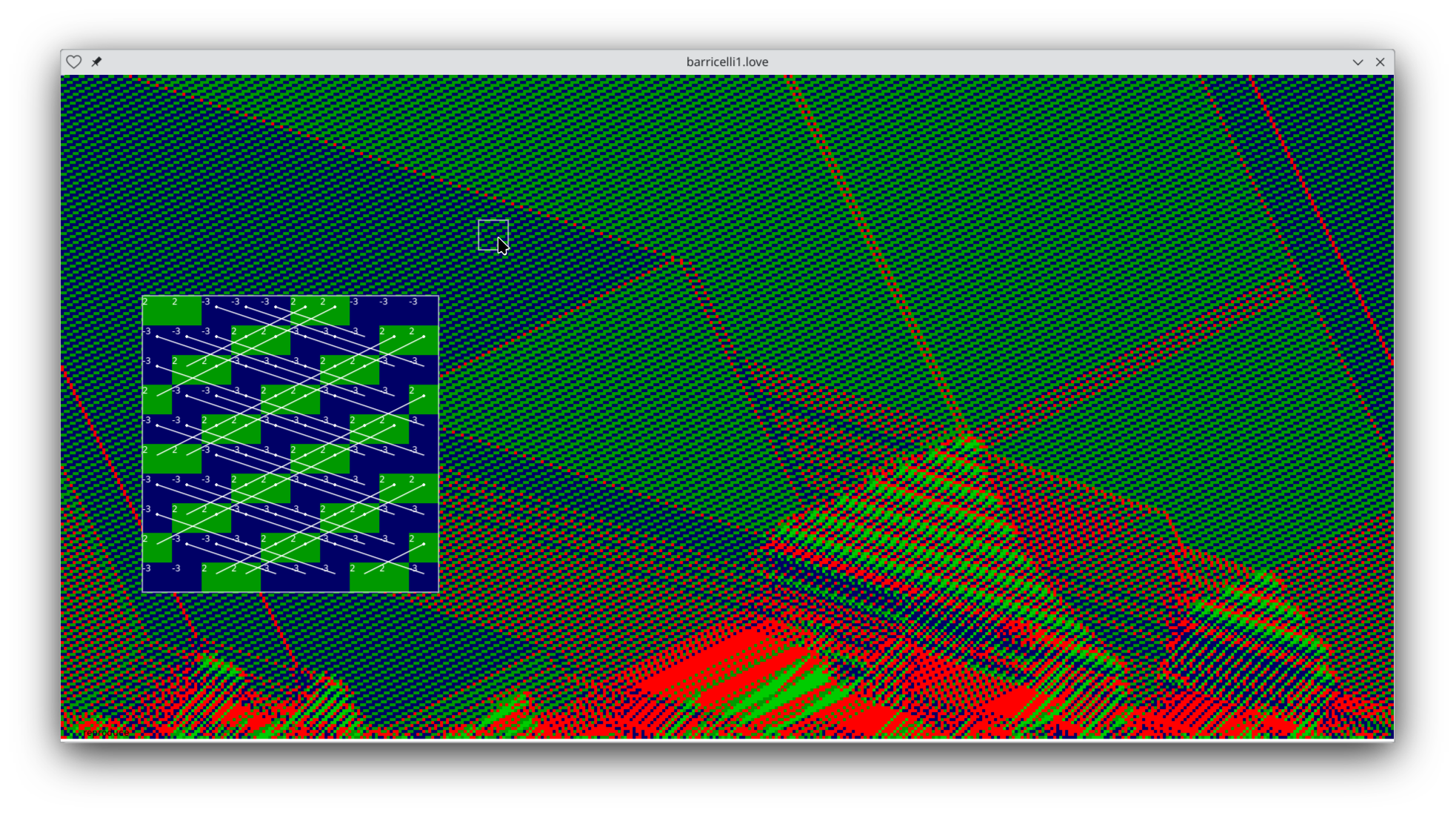
Very similar phenomenon of groups of like elements "switching partners."

One example that suggests why these patterns robustly occur is to introduce a single empty (red) square into a field of BBBGG. What we see is the empty square "move" leftwards at a rate of 3 squares per time step — and it leaves to its right a growing field of BBGGG. Similar effect to a catalyst or enzyme.

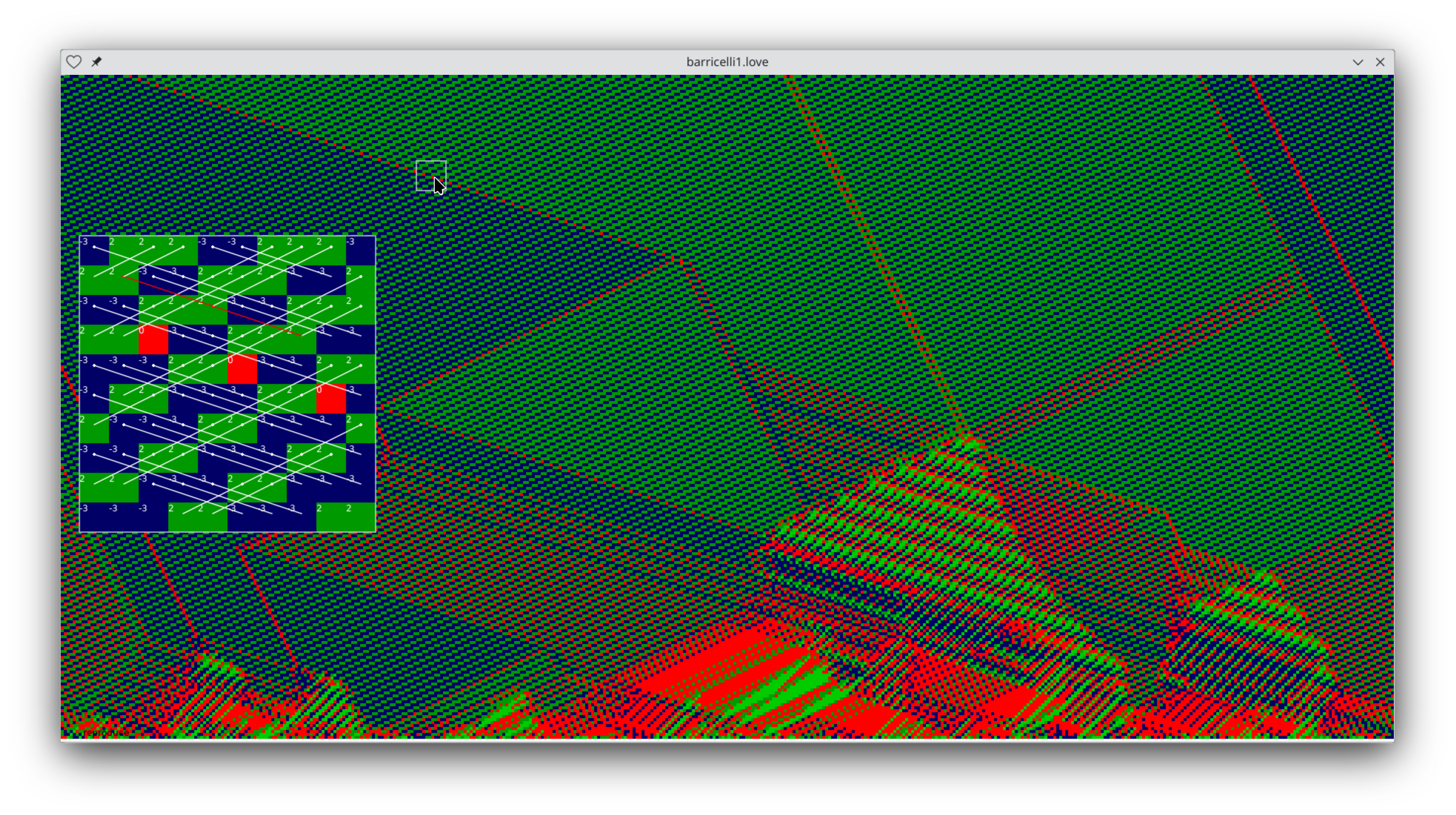
The consistency with which periodic patterns occur is largely due to the balance between creation and destruction rules. Here's a different and much more complex periodic pattern elsewhere in the same space:

This is a complex pattern with a period of 25 squares, and for its stability it requires both destruction (places where the white lines of movement intersect, annihilating colliding elements) and creation (red lines that cause a square to create a second copy of itself).

Open questions

• I haven't dug into the third rule (mutation) yet to understand its effects in detail.
• Barricelli describes complex organisms arising from a random field of just +1s and -1s (i.e. elements striding 1 element leftward or rightward), but I have a simple proof that that can't happen with the rules as I've described them above. I'd like to understand how to tweak the rules to reproduce this result.
• Barricelli describes patterns that aren't stable by themselves, but can spread in the presence of "host patterns". He calls these parasites, though it may be more precise to compare them to viruses. I'd like to reproduce some of the patterns he mentions.

Philosophical aside #1

One interesting claim Barricelli makes (pg 2): a pattern that reproduces itself tends to also propagate the environment that it arose in. If something about the environment caused an organism to spontaneously arise, almost by definition the organism is required to preserve that property to reproduce itself. So he claims that the insides of cells likely are very similar in some ways to life on earth back when RNA spontaneously emerged. No way to be sure, of course, but the argument kinda hangs together for me. And the empirical evidence for this is that the Earth is 4.3 billion years old, and life on the earth is around 4 billion years old. Once conditions were right, life basically emerged in a cosmic eyeblink. One way to view all of later life is as ways to protect that initial environment in the face of more and more hostile environment changes, to create little bubbles of the primordial soup inside us all.

And it's fractal. As new structures arise to protect old bubbles, they are themselves self-propagating and they need their own environments preserved.

A specific property of the environment isn't necessarily helpful to all life. One organism may need some environmental property that another organism finds utterly hostile. Just by being first, an organism will tend to propagate the environment it needs. And by doing so it's competing with even the possibility of other organisms that don't exist yet.

This line of thought leads me to wonder if it may be easier than I thought to find new conditions suitable for the emergence of life. I know physicists run large simulations of the early universe on supercomputers, which generate plausible compositions of elements over time as supernovas occur. I also vaguely remember from TV programs long ago that we've tried to run simulations of earth's primordial soup using best guesses of its early composition. What if we put these two ideas together? Given a simulation of the early cosmos, generate candidate stars, candidate planets around those stars, plausible initial distributions of elements on those planets, conditions of temperature and pressure. Then simulate brief slices of time. If (my interpretation of) Barricelli is correct, life either emerges instantly or not at all, and we may be able to try out a variety of conditions relatively cheaply. And maybe identify candidate chemistries that help molecules reproduce.

There's probably some professor somewhere who is aware of past research in this vein and can point me at papers :)

Philosophical aside #2

One way to view the story of our evolution is as a leveling-up of goals:

• Life: "cells maintain the environment in which RNA molecules originated."
• Bureaucracy: you create a system that can outlive you. The system outlives its own usefulness.
• Permaculture: design systems to try to make themselves less and less necessary to the functioning of the ecosystem.

Credits

Some example code from Simone Conradi and some pointers to literature from Karsten Schmidt got me going. This paper was my primary source.

This post is part of my Freewheeling Apps Devlog.

Comments gratefully appreciated. Please send them to me by any method of your choice and I'll include them here.