Umpteenth attempt at stripping away unnecessary rules when teaching programming.

(Just a mockup to convey the idea. Plan is just to use this notation with pen and paper.)

Is this picture intelligible without any explanation?

permalink

Here's the most recent bugfix I had to make, along with a fairly lengthy but still incomplete post-mortem in the commit description.

Still several things left to investigate.

• Really small windows probably crash.
• Really wide and short windows probably crash.
• Pressing and releasing mouse really quickly within a single frame will probably crash.

I want to delete some data structures and just recompute them all the time.

permalink

All the bugs in my software that others run into have the following story template:

• t = n: my program was responsible for x and y
• t = nn: my program became responsible for x, y and z
• t = nnnnnn: bug in z (interacting with x/y)

Adding z required rethinking the entire program. I tried to patch it in. Implications were not fully worked out.

permalink

Trying to build software for others is extremely disheartening. I can be eating my own dogfood on a daily basis for years and still newcomers hit bugs in their first 10 minutes.

I wonder if this is the major reason to huddle together on top of jenga stacks with tons of dependencies, terrified of fragmentation: You always need more testing than you think, and there's no way to compete with something that's been through that much testing.

I come stare at this abyss every year or two.

• 2022-03-31
• 2024-12-03

Doesn't do me any good, though.

(This post spawned a sprawling, constructive conversation.)

permalink

Visualizing the digits of π

The following program lets you scrub the mouse downward to find more and more precise approximations of π within the red optical sight in the center of the screen.

permalink

I've been idly looking at the space of possible rules for 1-D cellular automata.

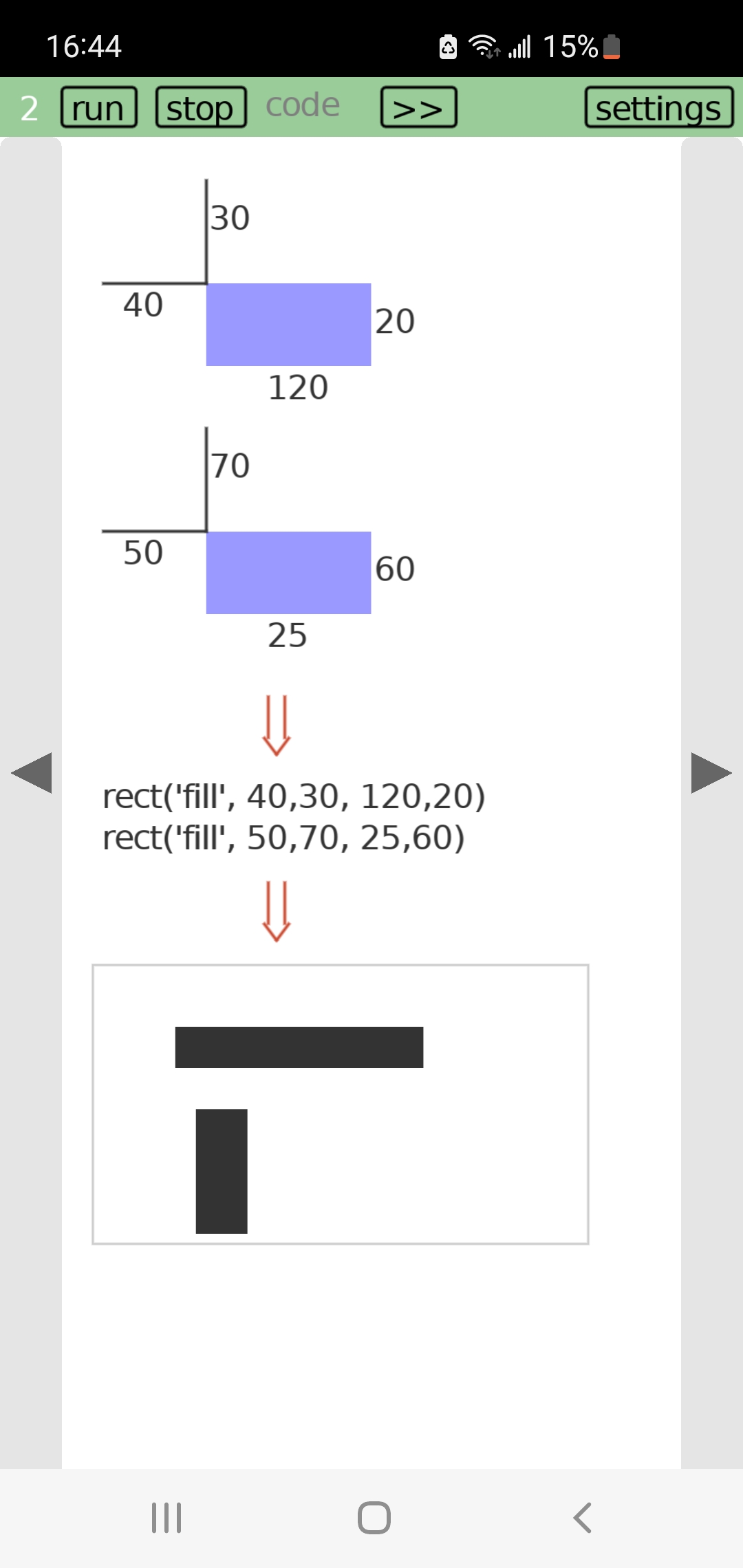
To recap, you basically have a line of cells that can be in one of two states ('alive' or 'dead') and rules that decide how a cell's state evolves based on the state of its immediate neighbors to the left and right. The images below show a snapshot of time in a row of pixels, and time advancing from the top row of pixels to the bottom.

Starting from a single live cell, of the 256 rules 16 immediately wink out (empty grids in the picture below), 16 don't change (vertical lines), 48 move the cell (24 each to the left and right), 30 grow into triangles over time (6 each to the left and right and 18 on both), 18 form Sierpinski patterns and 22 are more chaotic. Here's a detail in Lua Carousel where you can see many of these types.

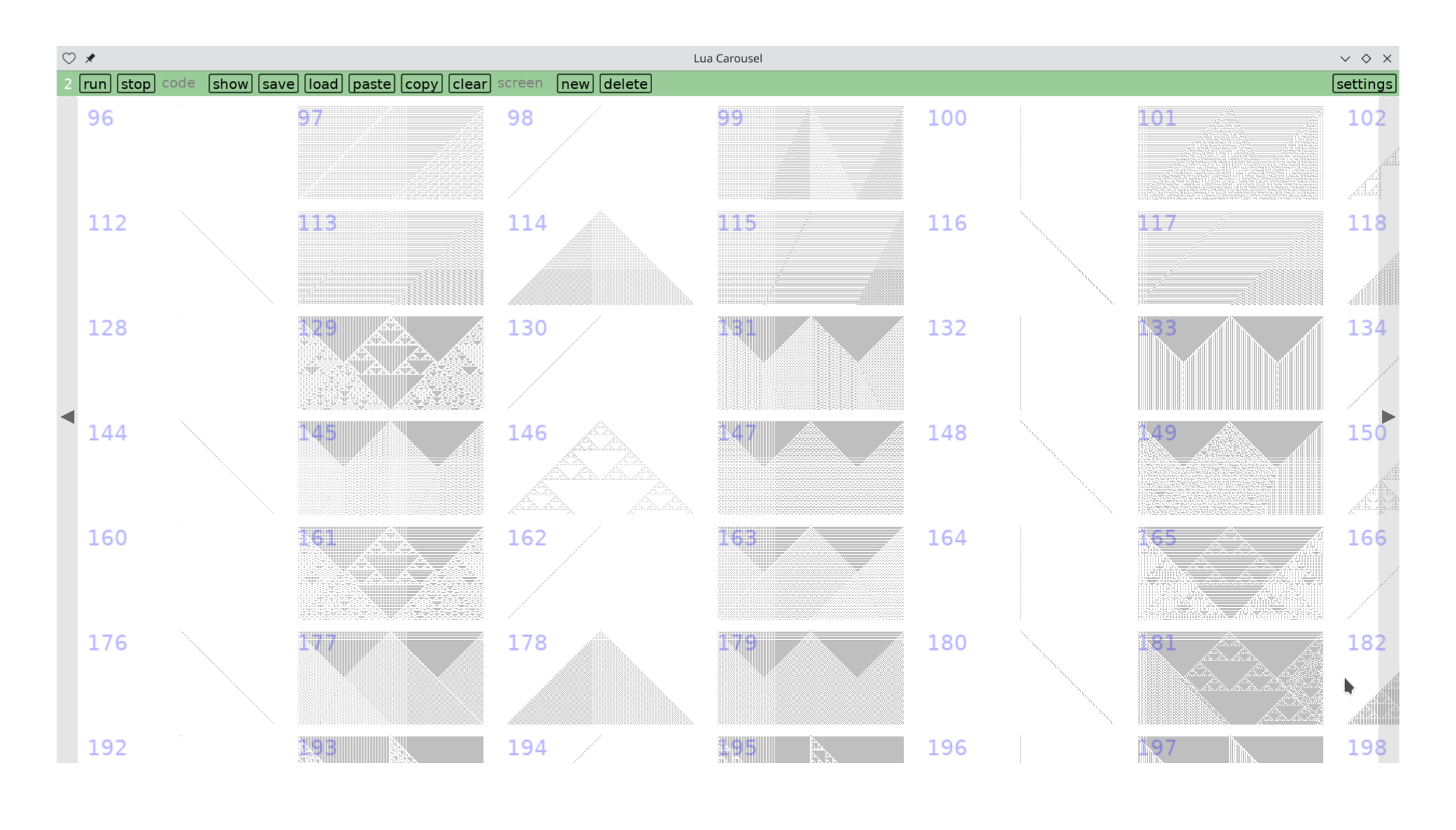
However, things look different if you start from a random configuration of live and dead cells. Seemingly well-behaved rules hide subtleties, and seeming patterns vanish. Read more →

The kids got a choose-your-adventure Oregon Trail book from the library, and I got nerdsniped into making a map for it.

(It's easy to get me to do something if it involves opening snap.love)

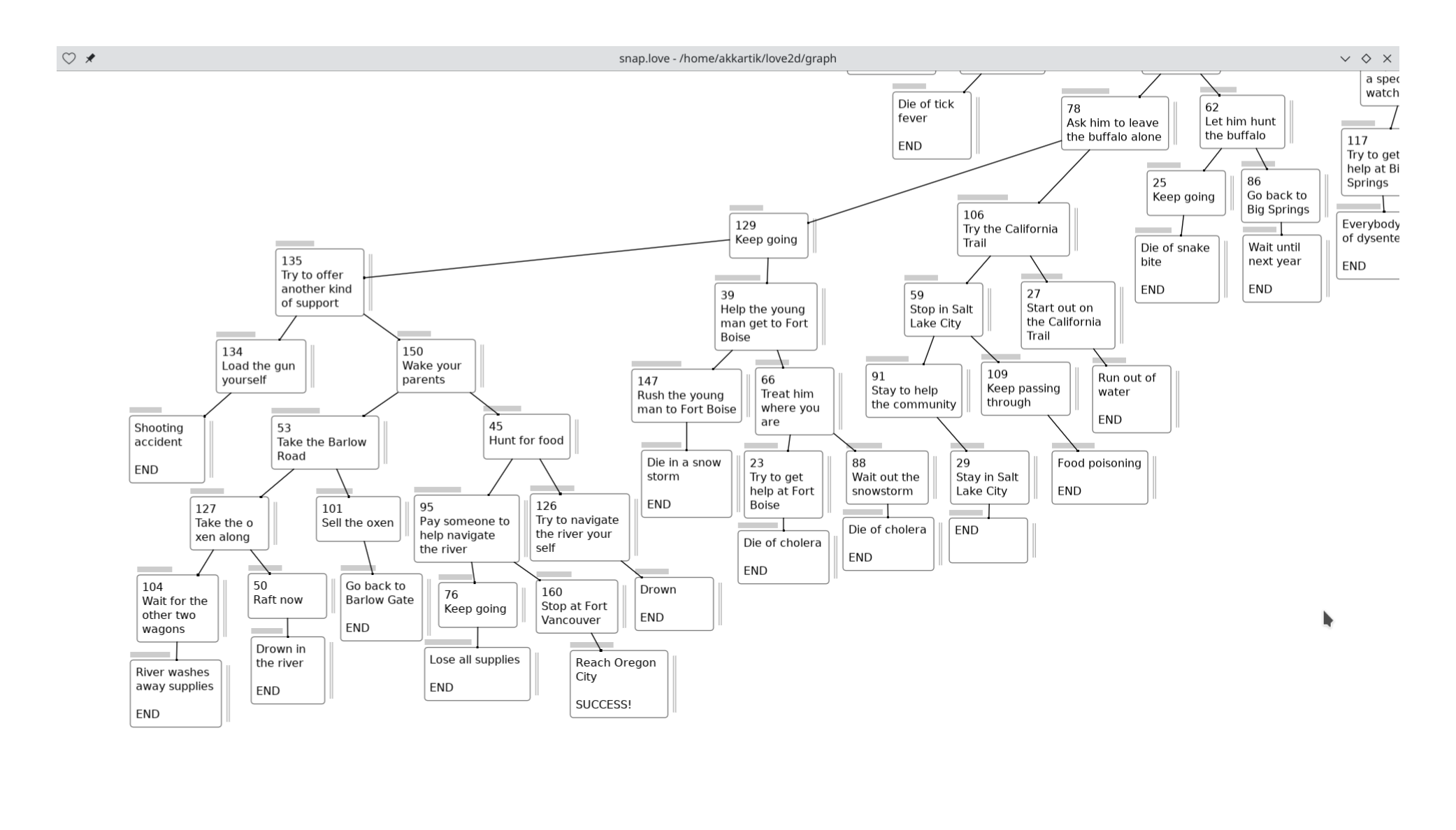
After finishing the map, I've been paying attention to the "meta game" of manually adjusting box positions and widths (height depends on amount of text) to make the arrangement pleasing to the eye. Constraints I've grown conscious of during this process:

• Lining up child nodes vertically
• Lining up nearby nodes. (imperfectly)
• Avoiding long edges.
• Keeping nearby edges approximately the same length.

I'd appreciate if anything seems jarring in this image, or if you have new OCD rules to infect me with :)

One frustration: I spent a while adjusting widths of boxes to not wrap lines within words, only to find that adjusting zoom messes things up again. This is an old problem: I can have precise scaling or crisp text, but not both. All my apps choose the latter.

permalink

I'm reading a paper on my phone in bed and see this problem:

Convolving a list with itself. Given a list [x1, x2, ..., xn−1, xn], where n is unknown, construct [(x1, xn), (x2, xn−1), ..., (xn−1, x2), (xn, x1)] in n recursive calls.

And I am able to switch apps and solve it right on my phone, without needing to get out of bed.

I do have to put up with some klunky (Lua) syntax, though.

permalink

New convivial platform just dropped

Looks like it's a fork of emscripten augmented to compile a whole OS kernel and userland. Includes raylib for graphics, and Lua bindings to it so I feel at home. Seems easy to build so I'm comfortable depending on the hosted version.

There's an app store anyone can publish apps to. Your changes remain in your browser's local storage until you publish them. All apps in the app store are mounted on the file system under /usr/store so it's easy to look at their source code.

Here's a port of one of my early LÖVE apps, for geometric constructions. It's on the app store so anyone should be able to run it just by clicking on this link.

Disclaimers. It's slow. Still lots of bugs. I had to reboot the VM several times while recording this video. Commands often hang or crash, then completely stop working until I reload. It's never lost my data, though. (Data is stored in local storage.)

permalink

Drawing histograms

From the Lua Carousel devlog.

permalink